...
COA Lec 09 Describe the Von Neumann Model and explain the functioning of its components | COA previous years...
COA Lec 08 Software in Hindi Video | System | Application | Programming | Computer Organization Architecture
Java lect 42 Inheritance types single, multilevel, hierarchical etc. in Hindi Video lec | Campus placement
lect 27 Parameterized methods in Java same name different parameter Campus placement preparation in Hindi Video
Lect 03 Declaration, initialization, display of variable in Java in Hindi video lecture
Lect 03 Declaration, initialization, display of variable in Java video lecture in Hi...
Lect 02 Understanding public static void main (String args[] ){ } in Jav...
Lect 02 Understanding public static void main (String args[] ){ } video lecture in Java in Hi...
In a town of 10000 families, it was found that 40% families buy product A, 20% buy product B
DAVV MBA PYQIn a town of 10000 families, it was found that 40% families buy product A, 20% buy product B and 10% buy product C, 5% buy product A and product B, 3% buy product B and product C and 4% buy product A and product C. If 2% families buy product A, B, C all. Then find the number of the families...
In a managers club, 45 play polo, out of which 30 play Polo only
DAVV MBA PYQIn a managers club, 45 play polo, out of which 30 play Polo only 28 play Snookers. 25 play Tennis of which 11 play Tennis only, 7 play Tennis and Polo, but not Snooker. 5 play Polo and Snooker, but not Tennisi) How many play all the thre sports?ii) How many play Snookers only?iii)...
In a survey of 500 T.V. viewers, 285 watched KBC, 195 watch cricket, 115 watch hockey, 45 watch KBC and hockey
DAVV MBA PYQIn a survey of 500 T.V. viewers, 285 watched KBC, 195 watch cricket, 115 watch hockey, 45 watch KBC and hockey, 70 watch KBC and cricket, 50 watch cricket and hockey, 50 do not watch any of three games. How many watch all 3 and how many watch exactly one of three ?Solution:K for KBCH for...
In a city there are 100000 people, 64% of them speak Greek, 55% people speak Latin, 43% p
DAVV MBA PYQIn a city there are 100000 people, 64% of them speak Greek, 55% people speak Latin, 43% people speak French, 21% people speak both Greek and Latin, 31% people speak both Greek and French, and 41% people speak both Latin and French. Determine the number of people speak all the three languages.Solution:G for GreekL for LatinF for FrenchFormula: n(G U L U F) = n(G)+n(L)+n(F)-n(G ∩ L)-n(G...
A company studies the product preferences of 20,000 consumers. It was found that each
DAVV MBA PYQ A company studies the product preferences of 20,000 consumers. It was found that each of the products A, B and C was liked by 7020, 6230 and 5980 respectively. All products were liked by 1500. Products A and B were liked by 2580, products A and C were liked by 1200 and products...
Write short note on 'Venn Diagram'. Illustrate your answer with suitable example.
DAVV MBA PYQWrite short note on 'Venn Diagram'. Illustrate your answer with suitable example.Solution: A venn diagram is a visual technique which shows relationship between Universal set, their sub-sets and certain operations on se...
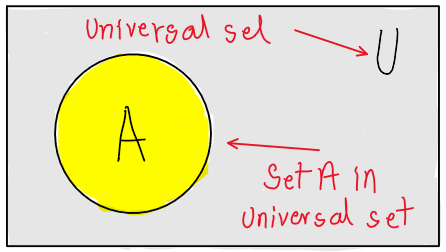
What is Set? Describe different types of sets
DAVV MBA PYQWhat is Set? Describe different types of sets.ORDefine the following with suitable examples:Finite setInfinite setUniversal setPower setProper subsetCardinal Num...
C Program GATE 2018 -8
Consider the following C code. Assume that unsigned long int type length is 64 bits.unsigned long int fun(unsigned long int n){ unsigned long int i, j = 0, sum = 0; for (i = n; i > 1; i = i/2) j++; for&...
C Program GATE 2018 -7
Consider the following C program:#include<stdio.h> void fun1(char *s1, char *s2){ char *tmp; tmp = s1; s1 = s2; s2 = tm...
Develop a Gantt Chart, Average Waiting time, FCFS, SJF, RR
RGPV 2020 CPU Scheduling AlgorithmConsider the following set of processes.
Process
Burst Time
Arrival Time
P1
3
0
P2
5
1
P3
2
2
P4
5
3
P5
5
4
Develop a Gantt-chart and calculate the average waiting time using:i) FCFSii) SJFiii) Round...
TCS Coding Q-01
TCS NQTQ. An automobile company manufactures both a two wheeler (TW) and a four wheeler (FW). A company manager wants to make the production of both types of vehicle according to the given data below:1st data, Total number of vehicle (two-wheeler + four-wheeler)=v2nd data, Total number of wheels = WThe task is to find how many two-wheelers as well as four-wheelers need to manufacture as per the given...
C Program GATE 2019 -4
C Program : GATE 2019Consider the following C program:#include <stdio.h> int main(){float sum = 0.0, j = 1.0, i = 2.0; while (i/j > 0.0625){j = j + j;sum = sum + i/j;printf("%f\n", sum);}return 0;}The number of times the variable sum will be printed, when the above...
C Program GATE 2019-2
C Program : GATE 2019Consider the following C function.void convert(int n){ if(n<0) printf(“%d”,...
C Program GATE 2019-1
C Program : GATE 2019Consider the following C program #include <stdio.h>int main(){ int arr[]={1,2,3,4,5,6,7,8,9,0,1,2,5}, *ip=arr...
C Program GATE 2019-6
C Program : GATE 2019Consider the following C program:#include <stdio.h>int jumble(int x, int ...
If cache access time is 100ns, main memory access time is 1000ns and the hit raio is 0.9. Find the average access time and also define hit ratio.
If cache access time is 100ns, main memory access time is 1000ns and the hit raio is 0.9. Find the average access time and also define hit rat...
Visual Basic Database Connection and Insert Query
How to create database connection in Visual Basic ?Here, we are going to use Visual Basic 2010 and MS Access 20...
Consider the following employee database
Consider the following employee database. (RGPV 2019)Employee (empname,street, city) work (empname,companyname,salary) company (companyname,city) manages (empname,management). Give an expression in the SQL for each reque...
Explain the concepts of Generalization and Aggregation with appropriate examples.
Explain the concepts of Generalization and Aggregation with appropriate examples. (RGPV 2019)Ans. Generalization:Entities with common attributes can be merged into a generic or super type entity by generalisation. For example, the entity EMPLOYEE is a super type of Professor, Conductor, and Engine...
Function in C Programming
C Programming | Function Comment, if answer to the questions highlighted in red are correct, or not. Or if any suggesti...
In PERT/CPM, the merge event represents | UGC NET
UGC NET 2018 : In PERT/CPM, the merge event represents _____ of two or more even...
Time Complexities of sorting algorithms
Algorithm
Time Complexity
Best case
Average case
Worst case
Bubble
Sort
Ω(n)
θ(n2)
O(n2)
Bucket
Sort
Ω(n+k)
θ(n+k)
O(n2)
Heap
Sort
Ω(n
log(n))
θ(n
log(n))
O(n
log(n))
Insertion
Sort
Ω(n)
...
Find the time complexity of sum of two numbers using function
What is the time complexity of the program for the sum of two numbers using function...
Software coupling involves dependencies among pieces of software | UGC NET
UGC NET 2018 : Software coupling involves dependencies among pieces of software called modules. Which of the following are correct statements with respect to module coupling?&nb...
Process in Main Memory and Ready and Waiting for execution is kept on | UGC NET
UGC NET 2018 : A process residing in Main Memory and Ready and Waiting for execution, is kept on &nb...
How many people completed the survey form | UGC NET
UGC NET 2018 : A survey has been conducted on methods of commuter travel. Each respondent was asked to check Bus, Train or Automobile as a major method of travelling to work. More than one answer was permitted.&nb...